Recently, a friend asked in a chat if it would be possible to recover their password which was encrypted with a PIN code they forgot. They saved it as a backup, but while resetting their PC, forgot both the password and the PIN used to encrypt it. I asked what encryption method was used, and they did not know, so I knew I was in for an adventure.
After extracting some more clues, and eventually reverse-engineering the online encryption website, I was able to reproduce the algorithm locally to brute force the PIN successfully!
Clues
Let's start with the ciphertext (replaced for privacy), which should decrypt to a 30-character random password:
The person in need told me they thought it was encrypted using a 4-digit PIN, but that it could be longer. Other than that, no more information, so saying this is a shot in the dark would be an understatement. To brute force a ciphertext like this we should have the algorithm used to encrypt/hash it and then simply run that algorithm with random PINs until it decrypts successfully, and we should have a plaintext.
After some more questions, they found a Google search of "encrypt text with key" close to when they had encrypted the text. Doing this search now gave the following site as the first search result:
https://www.devglan.com/online-tools/text-encryption-decryption
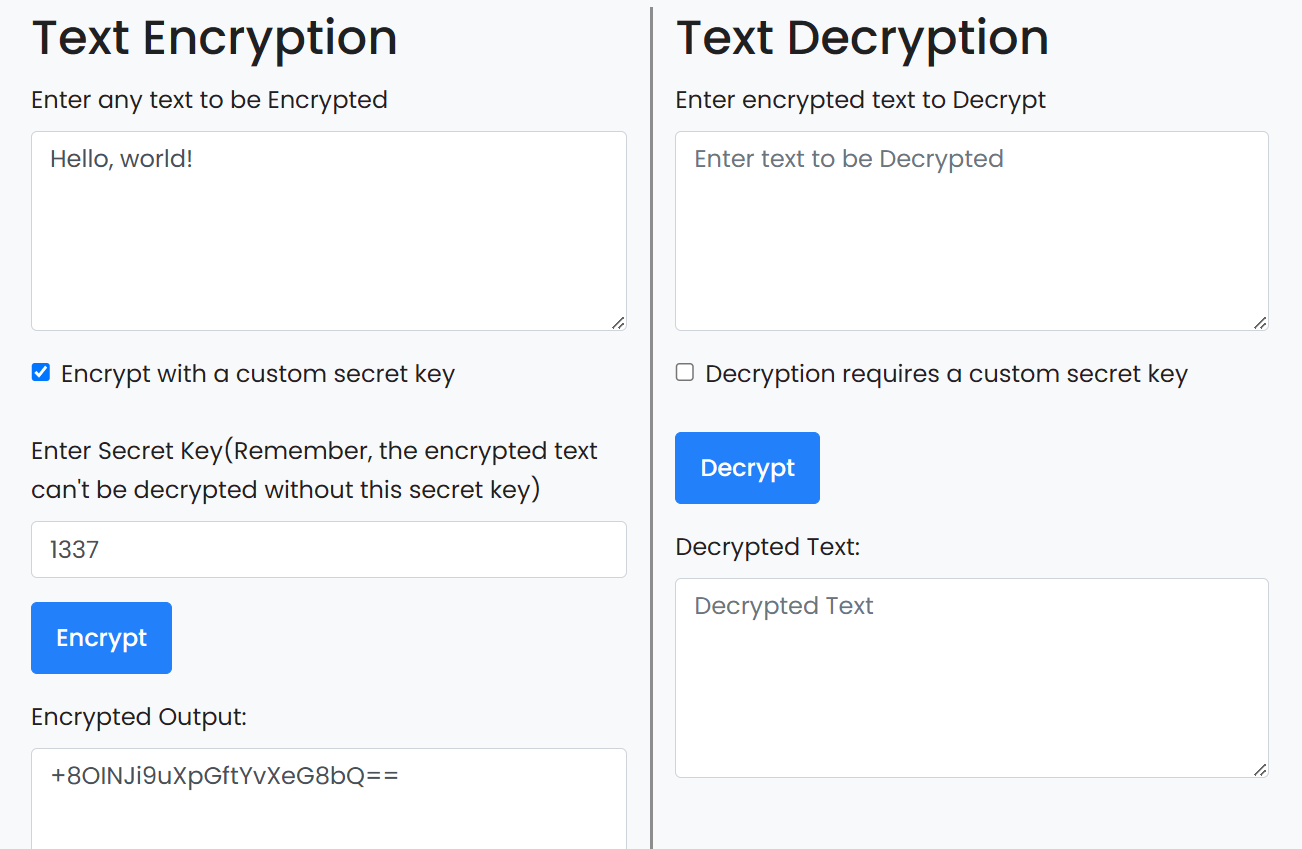
It allows inputting a plaintext, and optionally adding a secret key like a numeric PIN. This is a good candidate for the website they would have used. Now the question becomes: How does the website work?
What cipher mode was used?
Finding out exactly how this website worked was the biggest task. After a small amount of OSINT, I could not find the source code or any more details about its workings, so we have to deal with just this website's input and output. Luckily, cryptographic algorithms have some characteristics that we can test for to make more educated guesses about what exact algorithm is used.
A common and simple way of encrypting data is using Block ciphers where AES is the most widely used. These block ciphers work in chunks of 16 bytes and only ever output in lengths that are a multiple of 16. If your input is not, it will be padded with some other characters until it is. We can check if the site uses a block cipher by inputting a text shorter than 16 characters, and one slightly longer than 16 characters, to see how large the output gets after decoding it from Base64:
15: 123456789012345 -> s3BZfVerjOoHeoK4Prp8hQ== (16 bytes)
16: 1234567890123456 -> Vv0nGPawVaDI8YjukSAmTrKt30IxDw9bjSemeqazp4I= (32 bytes)
17: 12345678901234567 -> Vv0nGPawVaDI8YjukSAmTswOEW1aNLeU1CawMDkM0LY= (32 bytes)
The above clearly shows a large jump from 15 to 16 bytes, but you may have expected this jump to occur one later from 16 to 17 bytes because 16 bytes of plaintext should fit into 16 bytes of ciphertext. The reason for this is the magic padding that is added whenever a plaintext is not long enough. Using the standard PKCS#7 scheme will fill the remaining bytes with the number of remaining bytes, for example:
AA AA AA AA AA AA AA AA AA AA AA AA AA AA AA 01 (1 byte missing)
AA AA AA AA AA AA AA AA AA AA AA AA AA 03 03 03 (3 bytes missing)
AA AA AA AA AA AA AA AA AA AA AA AA AA AA AA AA 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 (16 bytes missing)
As you may notice in the above, when the last block of the plaintext is exactly 16 bytes, padding will still be added as 16 bytes in the next block! This is to avoid confusion while unpadding the plaintext during decryption because if this padding did not exist in this last block, the decoder would find AA as the last byte, and potentially mistake it for a padding byte. That's why we find that our 16-byte input already gives a 32-byte output, and we can be certain that this website is using a block cipher.
Block ciphers have various Modes of operation that use the single-block encryption algorithm like AES and turn it into a multi-block algorithm or even a stream cipher. The simplest has to be ECB:
It directly passes the plaintext in chunks of 16 through the same encryption box with a secret key, and outputs are directly appended to each other. One well-known problem this causes is that every equal 16 bytes of input will lead to the same 16 bytes of output. This may sound like a small issue, but it allows discerning one block of data from the next and finding where they are the same to discover patterns. The example below shows this with encrypting pixels:
We can test for this behaviour in the website by inputting two of the same blocks, and seeing if they result in the same blocks of ciphertext:
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA (32x 'A') -> Dysxg8J1Xuj1Wt3wgrKT4jqRMSyCXNlZcRApP247wsfPfO0y+CR+RsGNEyPpIP1t
00000000 0f 2b 31 83 c2 75 5e e8 f5 5a dd f0 82 b2 93 e2 |.+1.Âu^èõZÝð.².â|
00000010 3a 91 31 2c 82 5c d9 59 71 10 29 3f 6e 3b c2 c7 |:.1,.\ÙYq.)?n;ÂÇ|
00000020 cf 7c ed 32 f8 24 7e 46 c1 8d 13 23 e9 20 fd 6d |Ï|í2ø$~FÁ..#é ým|
As seen above, there are no duplicate blocks in this example so we know ECB is not being used here. There is one common alternative called CBC (Cipher block chaining) that works similarly to ECB, but sprinkles in some XOR of previous blocks to make sure no repetitions happen:
With this mode of operation, the decryption step is quite interesting. If we take any arbitrary ciphertext, we can flip any of its bits in what's known as a Bit-flipping Attack. This causes the decryption of the block we flipped a bit in to produce random garbage, but the block after it will use the input ciphertext to XOR its plaintext with, as part of CBC! Our bit flip in the previous block will then also flip a bit in the same position in the next block. This specific behaviour can also be tested for. If this "attack" works, we know we are dealing with a CBC mode of operation:
1. Generate some valid ciphertext
| | | |
Input: |Hello, world!AAA|AAAAAAAAAAAAAAAA|AAAAAAAAAAAAAA |
Output: |=???7?TY?????P??|???CQ?o?????=?pT|?~???]???ap??`?R|
2. Flip any of the bits, let's change `o` to `X`
| | | |
Flipped: |=???7?TY?????P??|???CQ?X?????=?pT|?~???]???ap??`?R|
Output: |Hello, world!AAA|q8???bD\?z_?;2??|AAAAAAvAAAAAAA |
As you see above, by flipping a character in the middle block, it turned into garbage and changed an A to a v in the last block! This must mean the website is using CBC mode.
Key padding
This is some good progress already, but the use of AES opens up some more questions. It uses either a 16-byte, 24-byte or 32-byte key for encrypting the individual blocks. However, we are able to input any number of bytes as the "secret key" on the site, and it continues to work. One good way they could have done this is using a Key derivation function (KDF) to generate an AES key from any length of input. This could be hard to guess, but let's test if this is the case.
A simple way is by inputting a giant key and comparing it with the same key after changing one of its last bytes. That way, we confirm if our last bytes matter or not. They should in a KDF, but may be truncated if some other method is used:
Key (64): AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
Output: W7Pq9c4spLcN3hnJLjk+qw==
Key (64): AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB
Output: W7Pq9c4spLcN3hnJLjk+qw==
Good news, the last bytes of the key don't seem to matter. Now let's find exactly where this limit is:
Key (32): AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB
Output: W7Pq9c4spLcN3hnJLjk+qw==
Key (24): AAAAAAAAAAAAAAAAAAAAAAAB
Output: W7Pq9c4spLcN3hnJLjk+qw==
Key (17): AAAAAAAAAAAAAAAAB
Output: W7Pq9c4spLcN3hnJLjk+qw==
Key (16): AAAAAAAAAAAAAAAB
Output: 1tkmQeJrej+GgMNfZdEiGg==
We see the key is truncated to exactly 16 bytes before being used (pretty bad for an encryption service), but now one question remains: how does it fill the key up to 16 bytes? My first guess was the PKCS#7 padding again, which I tried by sending the following JSON directly to the API:
If PKCS#7 padding is used, these should output the same ciphertext. But it turns out, the website gives two different outputs for these keys. This must mean they use some other way to fill the empty space. We can write a quick Python script to loop through all possible bytes and see what the empty byte is filled with:
import requests
from tqdm import tqdm
from base64 import b64encode
s = requests.Session()
HOST = "https://www.devglan.com/online-tools"
def visit_home():
"""Required for getting a valid session cookie"""
r = s.get(HOST + "/text-encryption-decryption")
if not r.ok:
raise Exception(r.text)
def encrypt(text, key):
data = {
"textToEncrypt": text,
"secretKey": key,
}
r = s.post(HOST + "/text-encryption", json=data)
if not r.ok:
raise Exception(r.text)
return r.json()["encryptedText"]
if __name__ == "__main__":
visit_home()
open_spot = encrypt("Hello, world!", "A"*15)
for i in tqdm(range(0, 256)):
encrypted = encrypt("Hello, world!", "A"*15 + chr(i))
if encrypted == open_spot:
tqdm.write(f"Found: {i} ({bytes([i])})")
break
This first generates a ciphertext without having specified the last byte of the key, and then tries appending all 256 possible bytes to check if they match. After running it, we find one match!
For some reason, our key is filled with a t character. This means the key AAAAAAAAAAAAAAA would be the same as AAAAAAAAAAAAAAAt, which can also be confirmed manually. It is not hard to extend this script and also find the 2nd-to-last padding character:
if __name__ == "__main__":
visit_home()
known = "t"
open_spot = encrypt("Hello, world!", "A"*14)
for i in tqdm(range(0, 256)):
encrypted = encrypt("Hello, world!", "A"*14 + chr(i) + known)
if encrypted == open_spot:
tqdm.write(f"Found: {i} ({bytes([i])})")
break
Running it, we find 116 (b't') again, could it be ts all the way down? Let's try A vs Attttttttttttttt:
Correct! Now we can correctly pad keys as well. It pads the key to 16 bytes with ts, truncating any extra bytes.
Recovering the IV
So far we know it uses AES in CBC mode, with a 16-byte key that is padded with 't' characters. One last step required before being able to replicate it locally is finding the Initialization Vector of the CBC cipher mode. As seen in the diagram earlier, it is used as the XOR block before the first real block as a start of the chain, because the first block has no previous block to XOR with. Sometimes this IV is random, but not for security reasons, it may also be static. An important note is that this same IV is required during the decryption step as well, which is why a randomly generated IV is often prepended to the ciphertext so it can be recovered later. In our case, though, we only have 16 bytes of output for 15 bytes of input, so there cannot be an IV hidden in here. It must be static.
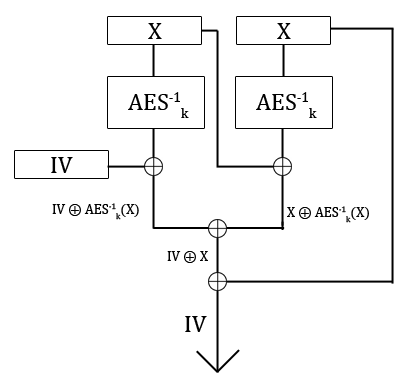
To find the IV, there are some clever tricks that abuse the logic of CBC. Take a look at the decryption step where the IV is directly XORed with the result from the first block AES decryption. This result is then the plaintext we receive:
Understanding the properties of XOR is crucial for the next trick, so let's start with a quick crash course on this. The operation works on bits and returns 1 if only one of the bits is 1, otherwise 0. Below is its truth table:
XORing bytes together simply means aligning the bits of one string with another and performing the XOR operation on each combination. As seen in the truth table above, you can also describe XOR as "flipping the bit if the other bit is a 1". This explanation makes it obvious that XOR-encrypting a "plaintext" with a "key", we are just flipping the plaintext bits where a key bit is 1, and a decryption just needs to flip them back. That means the decryption step will be the exact same operation as encrypting, neat.
When XORing a plaintext with a ciphertext in this way, we get 1 where these bits are different (0⊕1 or 1⊕0), and thus where they need to be flipped. This means the same thing as the key in our encryption, so XORing a plaintext and ciphertext will result in the key! This results in a scheme where XORing any two parameters will result in the third.
Back to AES, notice in the above that for the second ciphertext block, the same AES decryption takes place, creating the red intermediate value. But this time it is XORed with our first block of ciphertext. If we make the first two blocks of our ciphertext the same, both intermediate values will also be the same, only the XOR keys coming in from the side are different. For the second block, it is XORed with the first block's ciphertext which we know, so we can reverse the operation by simply XORing the plaintext with it again. Then we have the intermediate value from right after the AES decryption. This can finally be used in the first block of plaintext because we now know the intermediate and the first block of plaintext, so by XORing these two we get the IV back.
The diagram below shows this attack and how the IV flows out of it. Think through the steps for a little until it makes intuitive sense:
To see this in action, we can test locally that it really works:
from Crypto.Cipher import AES
from pwn import xor
KEY = b"A"*16
IV = b"I"*16
BLOCK = b"B"*16
cipher = AES.new(KEY, AES.MODE_CBC, iv=IV)
ciphertext = BLOCK * 2
plaintext = cipher.decrypt(ciphertext)
block1, block2 = plaintext[:16], plaintext[16:]
intermediate = xor(block2, BLOCK)
iv = xor(intermediate, block1)
print(iv) # b'IIIIIIIIIIIIIIII'
We can try this on the remote now, but quickly encounter an issue:
Ciphertext: AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA (QUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUE=)
Plaintext: "Error while decrypting the text"
When decrypting, the site likely validates the padding. The last byte of plaintext should be the padding byte, the value of which is how many padding bytes there are. It is common to check if all the bytes before it are also filled with the padding value as they should with PKCS#7 padding. Our crafted ciphertext generates garbage plaintext output, which is unlikely to have valid padding. Unlikely does not mean impossible though, because all we really need is for the last byte to be 01, verifying only the last byte, which should succeed 1/256 times.
After doing so, we should be able to execute the attack above to get the IV all in one go. Let's script the decryption part as well to find a ciphertext and key that results in a plaintext with a 01 suffix by pure coincidence.
def decrypt(text, key):
data = {
"textToDecrypt": b64encode(text),
"deSecretKey": key,
}
r = s.post(HOST + "/text-decryption", json=data)
if not r.ok:
raise Exception(r.text)
decryptedText = r.json()["decryptedText"]
if decryptedText == "Error while decrypting the text":
raise Exception(decryptedText)
return decryptedText
if __name__ == "__main__":
visit_home()
BLOCK = b"\x00"*16
ciphertext = BLOCK * 2
for i in tqdm(range(0, 1000)):
# Iterate over key values
try:
plaintext = decrypt(ciphertext, str(i))
except Exception as e:
if "Error while decrypting the text" in str(e):
continue
raise
# Until one decrypts successfully
tqdm.write(f"Key: {i}, Plaintext: {plaintext!r} ({plaintext.encode()})")
break
Running this, we quickly get a hit:
Key: 10, Plaintext: '&�ۛ�h���>�a��H6\x13���Q탐Y�\x03ξ~' (b'&\xef\xbf\xbd\xdb\x9b\xef\xbf\xbdh\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbd>\xef\xbf\xbda\xef\xbf\xbd\xef\xbf\xbdH6\x13\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbdQ\xed\x83\x90Y\xef\xbf\xbd\x03\xce\xbe~')
The goal of this was to extract the first and second 16-byte blocks of plaintext from this output. The printed part with question marks looks hard to copy, so we will take the b'...' bytestring and decode it after, but checking its length, we see something strange:
>>> b = b'&\xef\xbf\xbd\xdb\x9b\xef\xbf\xbdh\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbd>\xef\xbf\xbda\xef\xbf\xbd\xef\xbf\xbdH6\x13\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbdQ\xed\x83\x90Y\xef\xbf\xbd\x03\xce\xbe~'
>>> b.decode()
'&�ۛ�h���>�a��H6\x13���Q탐Y�\x03ξ~'
>>> len(b.decode())
26
In the response, the data is only 26 characters long... We can also notice that the question mark characters are all the same: Unicode character U+FFFD "Replacement Character", as well as other characters outside the 0-256 range:
>>> list(map(ord, b.decode()))
[38, 65533, 1755, 65533, 104, 65533, 65533, 65533, 62, 65533, 97, 65533, 65533, 72, 54, 19, 65533, 65533, 65533, 81, 53456, 89, 65533, 3, 958, 126]
It turns out that due to invalid UTF-8, a lot of characters get combined into a single multi-byte character or are replaced entirely by U+FFFD. We cannot work consistently with this, but luckily, the IV recovery trick does not require the full block correctly to get some info. We can go character-by-character filling in the ones we know now with valid 0-256 characters, or otherwise trying with another sample that does have that index. After a few tries, we should have them all.
The length problem is still tricky though. Removed characters will displace the index of future characters meaning we cannot be sure where they fall, and implementing a smart algorithm for that would be a lot of work. Instead, we can try to get lucky with a ciphertext where no characters are removed due to UTF-8 issues.
In our case, we expect only 1 character to be removed from padding, and the rest to stay, so we will look for 31-character long strings. This gets good candidates in a few more attempts:
for i in tqdm(range(0, 10000)):
# Iterate over key values
try:
plaintext = decrypt(ciphertext, str(i))
except Exception as e:
if "Error while decrypting the text" in str(e):
continue
raise
# If characters are missing, we don't know indexes for sure
if len(plaintext) != len(ciphertext) - 1:
continue
# Print if decrypts successfully
tqdm.write(f"Key: {i}, Plaintext: {plaintext!r} ({plaintext.encode()})")
Key: 439, Plaintext: '�\x10�,7��9\x1e~�\x06Z2!6�&�\x1a\x02��L&\x19�d,\x07\x17' (b'\xef\xbf\xbd\x10\xef\xbf\xbd,7\xef\xbf\xbd\xef\xbf\xbd9\x1e~\xef\xbf\xbd\x06Z2!6\xef\xbf\xbd&\xef\xbf\xbd\x1a\x02\xef\xbf\xbd\xef\xbf\xbdL&\x19\xef\xbf\xbdd,\x07\x17')
Key: 2385, Plaintext: '\x1dfy��;�g*��I1Q�6(PL��\x02�\x12\x12��+Gd�' (b'\x1dfy\xef\xbf\xbd\xef\xbf\xbd;\xef\xbf\xbdg*\xef\xbf\xbd\xef\xbf\xbdI1Q\xef\xbf\xbd6(PL\xef\xbf\xbd\xef\xbf\xbd\x02\xef\xbf\xbd\x12\x12\xef\xbf\xbd\xef\xbf\xbd+Gd\xef\xbf\xbd')
Key: 4508, Plaintext: 'b�7!�:�^�;*p���6W�\x02\x17�\x03�+�\\B\x12���' (b'b\xef\xbf\xbd7!\xef\xbf\xbd:\xef\xbf\xbd^\xef\xbf\xbd;*p\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbd6W\xef\xbf\xbd\x02\x17\xef\xbf\xbd\x03\xef\xbf\xbd+\xef\xbf\xbd\\B\x12\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbd')
Key: 5221, Plaintext: '4l��y\x00G�_\x14�/�P56\x01Z��L9.�gs�M�e\x03' (b'4l\xef\xbf\xbd\xef\xbf\xbdy\x00G\xef\xbf\xbd_\x14\xef\xbf\xbd/\xef\xbf\xbdP56\x01Z\xef\xbf\xbd\xef\xbf\xbdL9.\xef\xbf\xbdgs\xef\xbf\xbdM\xef\xbf\xbde\x03')
Key: 6963, Plaintext: '#�\x1ez�\x00�i��\x01�f\x14�6\x16�+L�9�\x1c��i�\x10!�' (b'#\xef\xbf\xbd\x1ez\xef\xbf\xbd\x00\xef\xbf\xbdi\xef\xbf\xbd\xef\xbf\xbd\x01\xef\xbf\xbdf\x14\xef\xbf\xbd6\x16\xef\xbf\xbd+L\xef\xbf\xbd9\xef\xbf\xbd\x1c\xef\xbf\xbd\xef\xbf\xbdi\xef\xbf\xbd\x10!\xef\xbf\xbd')
Key: 7112, Plaintext: '�#i��@\x1b\x14\x08�j\x103\x1fr6�\x15\\��yra0�\x02rE*D' (b'\xef\xbf\xbd#i\xef\xbf\xbd\xef\xbf\xbd@\x1b\x14\x08\xef\xbf\xbdj\x103\x1fr6\xef\xbf\xbd\x15\\\xef\xbf\xbd\xef\xbf\xbdyra0\xef\xbf\xbd\x02rE*D')
Key: 8785, Plaintext: '��]43�B�b"\x02�+�\x016��h\x02\x06�+�ZEj�]�7' (b'\xef\xbf\xbd\xef\xbf\xbd]43\xef\xbf\xbdB\xef\xbf\xbdb"\x02\xef\xbf\xbd+\xef\xbf\xbd\x016\xef\xbf\xbd\xef\xbf\xbdh\x02\x06\xef\xbf\xbd+\xef\xbf\xbdZEj\xef\xbf\xbd]\xef\xbf\xbd7')
These few working samples are enough to recover the Initialization Vector with certainty. Implementing the logic explained earlier, we only have to ignore characters outside the 0-256 range. We will replace them with ? question marks, but it seems like they cancel out. Then we replace the unknown \x00 bytes with ? in the output to get a nice visual of what characters we got:
import re
from pwn import xor
BLOCK = b"\x00"*16
def get_iv(block1, block2, pt):
tmp = xor(block1, block2)
iv = xor(tmp, pt)
return iv
results = [
b'b\xef\xbf\xbd7!\xef\xbf\xbd:\xef\xbf\xbd^\xef\xbf\xbd;*p\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbd6W\xef\xbf\xbd\x02\x17\xef\xbf\xbd\x03\xef\xbf\xbd+\xef\xbf\xbd\\B\x12\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbd',
b'\x1dfy\xef\xbf\xbd\xef\xbf\xbd;\xef\xbf\xbdg*\xef\xbf\xbd\xef\xbf\xbdI1Q\xef\xbf\xbd6(PL\xef\xbf\xbd\xef\xbf\xbd\x02\xef\xbf\xbd\x12\x12\xef\xbf\xbd\xef\xbf\xbd+Gd\xef\xbf\xbd',
b'b\xef\xbf\xbd7!\xef\xbf\xbd:\xef\xbf\xbd^\xef\xbf\xbd;*p\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbd6W\xef\xbf\xbd\x02\x17\xef\xbf\xbd\x03\xef\xbf\xbd+\xef\xbf\xbd\\B\x12\xef\xbf\xbd\xef\xbf\xbd\xef\xbf\xbd',
b'4l\xef\xbf\xbd\xef\xbf\xbdy\x00G\xef\xbf\xbd_\x14\xef\xbf\xbd/\xef\xbf\xbdP56\x01Z\xef\xbf\xbd\xef\xbf\xbdL9.\xef\xbf\xbdgs\xef\xbf\xbdM\xef\xbf\xbde\x03',
b'#\xef\xbf\xbd\x1ez\xef\xbf\xbd\x00\xef\xbf\xbdi\xef\xbf\xbd\xef\xbf\xbd\x01\xef\xbf\xbdf\x14\xef\xbf\xbd6\x16\xef\xbf\xbd+L\xef\xbf\xbd9\xef\xbf\xbd\x1c\xef\xbf\xbd\xef\xbf\xbdi\xef\xbf\xbd\x10!\xef\xbf\xbd',
b'\xef\xbf\xbd#i\xef\xbf\xbd\xef\xbf\xbd@\x1b\x14\x08\xef\xbf\xbdj\x103\x1fr6\xef\xbf\xbd\x15\\\xef\xbf\xbd\xef\xbf\xbdyra0\xef\xbf\xbd\x02rE*D',
b'\xef\xbf\xbd\xef\xbf\xbd]43\xef\xbf\xbdB\xef\xbf\xbdb"\x02\xef\xbf\xbd+\xef\xbf\xbd\x016\xef\xbf\xbd\xef\xbf\xbdh\x02\x06\xef\xbf\xbd+\xef\xbf\xbdZEj\xef\xbf\xbd]\xef\xbf\xbd7',
]
for d in results:
d = d.decode()
d = re.sub('[^\x00-\xff]', '?', d)
# Extract blocks, and add the stripped padding byte
block1, block2 = d[:16], d[16:] + "\x01"
assert len(block1) == len(block2) == 16
iv = get_iv(block1, block2, BLOCK)
print(iv.replace(b"\x00", b"?"))
From these results, we can pretty clearly see what the whole IV must be by combining the letters:
b'5?56?9?u?ghb???7'
b'565??9?u8??bv5?7'
b'5?56?9?u?ghb???7'
b'56??59i?8g?b?567'
b'5?56?9?u??h?v5?7'
b'?65??9iu8?hbv567'
b'??565?i?8gh?v?67'
-------------------
b'565659iu8ghbv567'
It must be 565659iu8ghbv567, looking down at your keyboard, you might be able to guess how this IV was generated :).
Brute Forcing locally
Because we think we now know everything there is to know about this algorithm, we can reproduce the whole thing locally. Using AES CBC with an IV of b'565659iu8ghbv567', and padding the key with ts until it has a length of 16.
Here is a full example of decrypting a string generated from this website:
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
from base64 import b64decode
IV = b"565659iu8ghbv567"
KEY = b"1337"
CIPHERTEXT = b"+8OINJi9uXpGftYvXeG8bQ=="
def pad_t(key, block_size=AES.block_size):
if len(key) == 0:
raise ValueError("Key must not be empty")
key = key[:block_size]
return key + b"t" * (block_size - len(key))
ciphertext = b64decode(CIPHERTEXT)
key = pad_t(KEY)
cipher = AES.new(key, AES.MODE_CBC, IV=IV)
plaintext = unpad(cipher.decrypt(ciphertext), AES.block_size)
print(plaintext) # b'Hello, world!'
The goal is of course to brute force the key of that specific ciphertext from my friend until it becomes a valid ASCII string. We can do this locally very quickly now:
CIPHERTEXT = b"gQTeM4DaMEFaK2hTXBiOOu4QuzyQbwcU6KrDcuGQ9zk="
def is_ascii(s: bytes):
return all(32 <= c <= 126 for c in s)
ciphertext = b64decode(CIPHERTEXT)
for i in tqdm(range(1000000)):
key = pad_t(str(i).encode())
cipher = AES.new(key, AES.MODE_CBC, IV=IV)
plaintext = cipher.decrypt(ciphertext)
try:
plaintext = unpad(plaintext, AES.block_size)
except ValueError:
continue
if is_ascii(plaintext):
tqdm.write(f"{i}: {plaintext}")
break
This takes a few second to run because Python isn't the fastest language for these kinds of calculations, but we find the PIN!
The code was 427556, which decrypts "gQTeM4DaMEFaK2hTXBiOOu4QuzyQbwcU6KrDcuGQ9zk=" into "yhNY^C9W3q2GbHPNufgcA$63L@mi3s". Found without making a million requests to the encryption server, and learning a lot about AES in the process.
I hope you enjoyed reading this as much as I did finding the solution. This shows once again that you should not trust these random websites, even if they are implemented securely, you are sending your "secret" data directly to their servers.